트위티의 열하일기
8장: 통계 모형화 [정리] 본문
1. 다중회귀
: 설명변수가 여러 개인 것
a. 다중선형회귀모형
- 편회귀계수: 기울기 b1, b2
2. 편회귀계수 (bi)
: x 이외의 설명변수를 고정한 채로 x가 1 늘어났을 때의 y 증가량
- 편회귀계수를 비교하기 위해 표준화편회귀계수 이용
- 표준화편회귀계수: 설명변수를 평균 0, 표준편차 1로 변환한 다음 회귀분석을 시행하여 구한 회귀계수
- 상관계수가 1에 가까운 강한 상관이 있을 때는 다중공선성이 있는지를 확인하고 이에 대처해야 함
3. 볌주형 변수
- 회귀분석의 설명변수가 범주형 변수라면 0, 1과 같은 가변수(dummy variable)로 바꿔서 설명변수로 이용

4. 공분산분석
: 일반적인 분산분석에 사용하는 데이터와 함께 양적 변수 데이터가 있는 경우에 후보가 되는 방법
- 공변량: 새로 추가한 양적 변수
- 사용조건 1) 집단 간 회귀의 기울기가 서로 다르지 않을 것
- 사용조건 2) 회귀계수가 0이 아닐 것

5. 차원과 데이터
: 차원이 늘어날수록 파라미터 추정에 필요한 데이터 양이 폭발적으로 증가한다 (차원의 저주)
- 차원이 증가할수록 다중공선성 문제가 일어나기 쉬움 → 모형의 추정 정밀도 떨어짐
- 대안: 차원축소 방법을 이용하여 차원을 줄임
6. 다중공선성
: 설명변수가 여러 개인 다중회귀에서 설명변수 사이에 강한 상관이 있는 경우, 다중공선성이 있다고 말한다
- 다중공선성이 있으면 추정값의 신뢰성이 떨어짐
- r이 1에 가까워질수록 추정오차가 커짐
- 추정값이 불안정할 때는 직선 관계에서 벗어난 값에 회귀계수가 영향을 받음으로써 회귀계수를 해석하기가 어려워짐


- 다중공선성 정도 측정
- 1. 분산팽창인수 VIF 계산
- VIF > 10: 두개 변수 사이의 상관이 아주 강함
- 다중공선성이 강하다고 판단되면, either 서로 상관이 있는 2개 변수 중 하나를 없앤다 or 차원 축서 방법을 통해 설명변수의 개수를 줄인다
7. 상호작용
: 설명변수 간의 상승효과. 선형회귀모형 안에서 곱셈 cx(i)x(j)로 도입할 수 있음
- 현실 데이터에서는 x가 1 증가했을 때의 y 증가 방식이 다른 설명변수의 영향을 받을 수도 있음
- 설명변수가 양적 변수인 다중회귀모형에 상호작용항을 넣을 것인지에 대한 판단은 다소 하기가 어려움
- 해석이 어려워짐
- 설명변수의 개수가 늘면 상호작용항의 수도 폭발적으로 늚
- 상호작용의 형태는 다양한데도 곱셈으로만 나타낸다는 한계가 있음
- 설명변수와 상호작용항의 다중공선성 문제가 있음
- 따라서 데이터에 분명한 상호작용이 있다는 것이 밝혀졌거나 기대될 때 사용하는 것을 추천
8. 이원배치 분산분석
: 두개의 요인이 있음을 고려할 때
- 가설검정 결과 상호작용항 c가 유의미하지 않다면 상호작용이 없다고 보고, 각각의 주효과를 그대로 평가


- 상호작용이 없다면 두 요인의 기울기는 평행
- 상호작용이 있다면 평행이 아님
9. 비선형회귀
: x에 관해 비선형인 모형

- 무턱대고 복잡한 모형을 채택하는 것은 바람직하지 않음
- 많은 경우 비선형회귀에서 최소제곱법으로 파라미터를 엄밀히 구할 수는 없으며, 컴퓨터를 이용해야 함
- 미분계수가 0이 되는 지점이 여러 개일 가능성도 있으므로 국소 최적해에 빠질 위험에 주의
10. 선형회귀 원리의 확장
a. 통계 모형화: 데이터 성질을 고려하면서 확률 모형을 가정하고, 파라미터를 추정하여 모형을 평가하는 일련의 작업
b. 일반선형모형 (general linear model)
- 설명변수가 양적 변수인 다중회귀부터, 설명변수가 범주형 변수인 분산분석까지를 포괄
c. 일반화선형모형 (generalized linear model)
- 최소제곱법이 아닌 확률분포에 기반한 최대가능도 방법으로 회귀모형 추정
- 더 폭넓은 유형의 반응변수를 대상으로 회귀분석 실행할 수 있음
- 베이즈 추정에 이용되는 계층적 베이지안 모형과 같은 유연한 모형화 가능해짐

11. 기능도와 최대가능도 방법
- 값이 2개인 반응변수 데이터나 음이 아닌 정수인 반응변수로 구성된 데이터는 거의 같은 값을 가지는 영역이나 데이터 퍼짐이 큰 영역이 있을 수 있음
- 이럴 때는 거리보다는 '확률적으로 얼마나 나타나기 쉬운가'에 기반해 데이터에 잘 들어맞는지 평가
a. 가능도
: P(x| θ)를 데이터 x에 대한 파라미터 θ 의 함수로 본 것
- 가능도가 크다 : 그 θ에서 얻은 데이터가 나타나기 쉽다
b. 최대가능도 방법 (최대가능도 추정)
: 가능도를 최대화하는 θ 찾고, 이를 추정값으로 삼으면 얻은 데이터에 가장 잘 들어맞는 파라미터 θ 정함
- 일반화선형모형은 반응변수 오차의 확률분포를 지정하고, 가능도를 이용하여 파라미터를 추정하는 회귀

12. 로지스틱 회귀
: 범주 하나가 일어날 확률을 p, 다른 하나가 일어날 확률을 1-p로 두고, 설명변수 x가 바뀌었을 때 p가 얼마나 달라지는지를 조사
- 반응변수가 값이 2개인 범주형 변수일 때 사용하는 회귀
- p는 이항분포의 파라미터에 해당

a. 이항분포

b. 로지스틱 함수
- 이항분포의 파라미터 p를 나타내기 적합함
- 수학적으로 쉽게 다룰 수 있음

c. 오즈비
: 2개의 확률 p와 q에 대한 2개의 오즈 비율
- 오즈(odds): 어떤 사건이 일어날 확률 p와 일어나지 않을 확률 1-p의 비율
- 오즈비 > 1: 확률 p가 확률 q보다 일어나기 쉬움

13. 푸아송 회귀
: 데이터가 음수가 되지 않는 정수일 때, 특히 반응변수가 개수인 경우 고려해볼 수 있는 일반화선형모형
- 푸아송 분포라는 확률분포를 따르는 회귀
a. 푸아송 분포
: 낮은 확률로 일어나는 무작위 사건에 대해, 평균이 i번일 때 몇 번 일어나는지를 나타내는 확률분포


14. 왈드 검정
: 최대가능도 추정량이 정규분포를 따른다고 가정했을 때, 왈드 통계량을 이용하여 신뢰구간이나 p값을 얻는 검정 방법
- 왈드 통계량: 최대가능도 방법으로 얻은 추정값/표준오차
- 표본크기 n이 크지 않을 때는 가능도비 검정이 더 신뢰도 높음
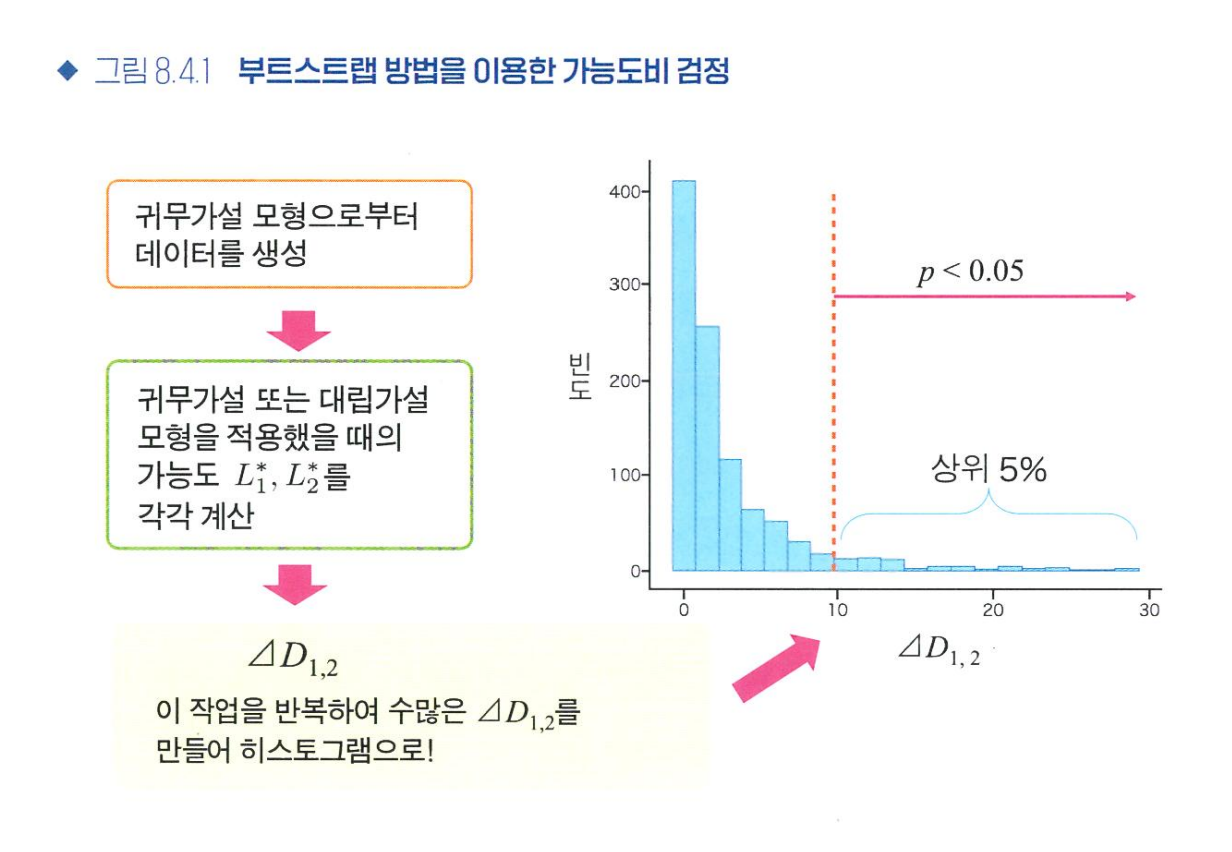
15. 가능도비 검정
: 최대가능도 방법으로 얻은 통계 모형을 비교하는 방법. 모형이 데이터에 잘 맞도록 개선되었는지 확인
- 전제) 비교할 2개의 모형 중 어느 한쪽이 다른 한쪽을 포함하는 관계여야 함
- 부트스트랩 방법: 어떤 가정하에 무작위로 데이터를 생성하고 추정량의 성질을 조사하는 방법
- 계산 방법: 아래 사진 참고
16. AIC
: 새롭게 얻을 데이터를 얼마나 잘 예측할 수 있는지를 바탕으로 모형의 좋음(적합도)을 결정하는 지표
- 모형의 최대가능도를 L, 모형의 파라미터 개수를 k로 하여 AIC = -2logL + 2k 와 같이 계산
- AIC가 작다는 것은 가능도가 크다는 뜻
- L이 같을 때는 파라미터 개수 k가 작을수록 AIC가 작아짐
- 파라미터 개수 k가 많은 모형일수록 실제 데이터에 잘 들어맞음 (적합도 높아짐)
- 과대적합: 실제 데이터에 무리하게 맞추는 바람에, 새롭게 얻은 데이터는 제대로 나타내지 못하는 상태
- (주의) 새롭게 얻을 데이터의 예측도를 높이는 모형을 고르는 것이 목적인 지표이므로, AIC를 최소화한다고 해서 그것이 반드시 실제 모형이지는 않을 수도 있음
16. BIC (베이즈 정보기준)
- 최대가능도 L, 파라미터 개수 k, 표본크기 n으로 하여 BIC = -2logL + klog(n)으로 계산
- BIC의 값을 최소화하는 것이 좋은 모형
- AIC와 다른 점: 표본크기 n에 따라 달라짐, 표본크기 n이 클수록 파라미터 개수 k의 패널티가 커짐
'Data Science > [도서] 통계101 데이터분석' 카테고리의 다른 글
| 10장: 인과와 상관 [정리] (1) | 2024.11.02 |
|---|---|
| 9장: 가설검정의 주의점 [정리] (1) | 2024.10.09 |
| 5장: 가설검정 [정리] (0) | 2024.09.24 |
| 4장: 추론통계~신뢰구간 [정리] (1) | 2024.09.24 |
| 3장: 통계분석의 기초 [정리] (0) | 2024.09.18 |




