6장: 다양한 가설검정 [정리]

6.1) 다양한 가설검정

가설검정 방법 구분해서 사용하기

- 가설검정은 해석 목적이나 데이터 성질에 따라 방법이 달라짐

- 다양한 가설검정 방법이 존재 -> 이 장이 다루는 내용

 

a. 가설검정 방법 선택 시 고려 요소 (3가지)

 

1. 데이터 유형

• 양적 데이터 & 볌주형 데이터 사이의 관계
• 범주형 데이터 & 범주형 데이터 사이의 관계
• 양적 데이터 & 양적 데이터 사이의 관계

 

→ 데이터 유형이 양적 변수인지 질적 변수인지에 따라 해석 방법이 달라지므로 데이터의 유형을 가장 먼저 확인해야 한다.

 

2. 표본의 수

• 데이터가 1표본일 때: 어떠한 2개의 변수 사이의 관계가 아닌, 1변수 데이터만을 조사
• 데이터가 2표본일 때: 두개 변수 사이의 관계를 조사. 특정 1개의 모집단분포에 대해 세운 가설을 검증하는 방식
• 데이터가 3표본 이상일 때: 다중비교 사용 (추후 설명)

 

3. 양적 변수 분포의 성질

• 데이터에 양적 변수가 있는 경우, 이것이 어떤 분포를 취하는지가 검정 방법을 선택할 때 중요하게 작용함
• 모수검정 & 비모수검정
• 등분산성 & 비등분산성

모수검정 (parametric test) : 모집단이 수학적으로 다룰 수 있는 특정 분포를 따른다는 가정을 둔 가설검정
- 모수검정의 대부분은 모집단의 분포가 정규분포인 경우 (데이터에 정규성이 있어야 함)

비모수검정 (nonparametric test) : 평균이나 표준편차 등의 파라미터(모수)에 기반을 두지 않는 방법
- 모집단분포가 특정 분포라고 가정할 수 없는 경우

 

등분산성: 분산이 같은 성질

부등분산성: 분산이 같지 않은 성질

 

 

6.2) 대푯값 비교

 

모수검정의 평균값 비교

* t검정은 모수검정의 한 검정 방법이기 때문에 데이터에 정규성이 있어야 한다

* 정규성: 데이터가 정규분포로부터 얻어졌다고 간주할 수 있는 성질

 

a. 일표본 t검정

• t 검정은 표본이 하나만 있어도 실행 가능 (표본이 2개면 이표본 t검정)
• 어떤 평균값의 모집단에서 표본을 얻었는지를 조사
• 계산 순서는 '평균값 95% 신뢰구간 구하기'와 같음

- 전제

- 귀무가설: "모집단의 평균은 μ = OO이다"
- 대립가설: "모집단의 평균은 μ = OO이 아니다"

 

 

b. 이표본 t검정

• 2개 집단의 평균값 비교
•  데이터의 분산이 일치할 때 (등분산성): t 검정
• 데이터의 분산이 일치하지 않을 때(비등분산성): 웰치의 t검정 (단, 이를 사용할 때도 정규성은 있어야 함)

- 전제

- 귀무가설: "2개 집단의 평균값은 같다" (평균값의 차이 = 0)
- 대립가설: "2개 집단의 평균값은 다르다" (평균값의 차이 != 0)

 

c. 대응 관계가 없는 검정 & 대응 관계가 있는 검정

 

1.  대응 관계가 있다

• ex. 신약 효과를 검증하는 실험 (신약 A, 구약 B)
• 피험자 20명 모두 A, B 약을 두 차례에 걸쳐 복용 & 검사

2.  대응 관계가 없다

• ex. 신약의 효과를 검증하는 실험
• 집단 1: "약 복용함" (n=10),  집단 2: "약 복용하지 않음" (n=20) 의 2개 집단 구분 → 총 n=20
• 이 2개 집단의 피험자들은 독립적인 관계. 대응 관계가 없음

- 대응 관계가 있는 데이터이면 똑같이 대응 관계가 있는 검정을 이용하는 것이 좋음

 

d. 정규성 조사

"모수 검정에서는 각 집단의 데이터에 정규성이 있어야 한다"

• 정규성 조사 방법: Q-Q 플롯 (시각적으로 판단 가능), 샤피로-윌크 검정 (가설검정으로 조사), 콜모고로프-스미르노프(K-S) 검정 (이론적인 분포와 비교)
• 해당 교재에서는 가설검정으로 시행

1.  전제

- 귀무가설: "모집단이 정규분포이다"
- 대립가설: "모집단이 정규분포가 아니다"

 

2. p-value 계산

→ p < 0.05: 귀무가설 기각, 모집단은 정규성이 없다

→ p >= 0.05: 정규분포에서 데이터를 얻었다고 적극적으로 주장하기는 어려움

(주의) 귀무가설을 기각할 수 없다고 해서 귀무가설이 옳다고 무조건적으로 판단할 수 없다!

 

 

e. 등분산성 조사

• 분산이 같다는 가설을 조사하는 검정: 바틀렛 검정, 레빈 검정

1. 전제

- 귀무가설: "2개 모집단의 분산은 같다"
- 대립가설: "2개 모집단의 분산은 같지 않다"

 

2. p-value 계산

→ p < 0.05이라면 부등분산

→ but, p > 0.05이더라도 적극적으로 분산이 같다고 주장할 순 없음 (정규성 검정과 같은 논리)

 

 

비모수검정의 대푯값 비교

a. 비모수 버전의 2개 표본 대푯값 비교

• 각 집단 데이터에 정규성이 없을 때 비모수검정 방법을 사용
• 비모수검정: 평균값 대신 대푯값에 주목 (분포의 위치에 초점을 맞춤)
• 비모수검정의 대표적인 방법: 윌콕슨 순위합 검정 (Wil-coxon rank sum test), 맨-휘트니 U 검정 (Mann-Whitney U Test), 플리그너-폴리셀로 검정 (Fligner-Policello Test), 브루너-문첼 검정(Brunner-Munzel test)

1. 윌콕슨 순위합 검정 (Wilcoxon Rank-Sum Test)

: 평균값 대신 각 데이터 값의 순위에 기반하여 검정을 실시

• 두 그룹의 데이터를 순서대로 정렬한 뒤, 각각의 순서를 부여함
• 각 그룹의 순위 합계를 계산하여 차이가 있는지 판단
• 정규분포를 가정하지 않기 때문에, 소규모 표본에서 유용하게 사용됨

2. 맨-휘트니 U 검정 (Mann-Whitney U Test)

: 두 독립된 그룹 간의 차이를 검정하는 비모수 검정

• 전제: 비교할 2개 집단의 분포 모양 자체가 같아야 함. (분산이 같지 않더라도 두 집단의 분포 모양이 비슷해야)
• 주로 윌콕슨 순위합 검정과 거의 동일하게 사용됨

 

분산분석 (3개 집단 이상의 평균값 비교)

- 3개 이상 집단의 평균값을 비교하는 방법: 분산분석 (ANOVA, Analysis of variance)

 

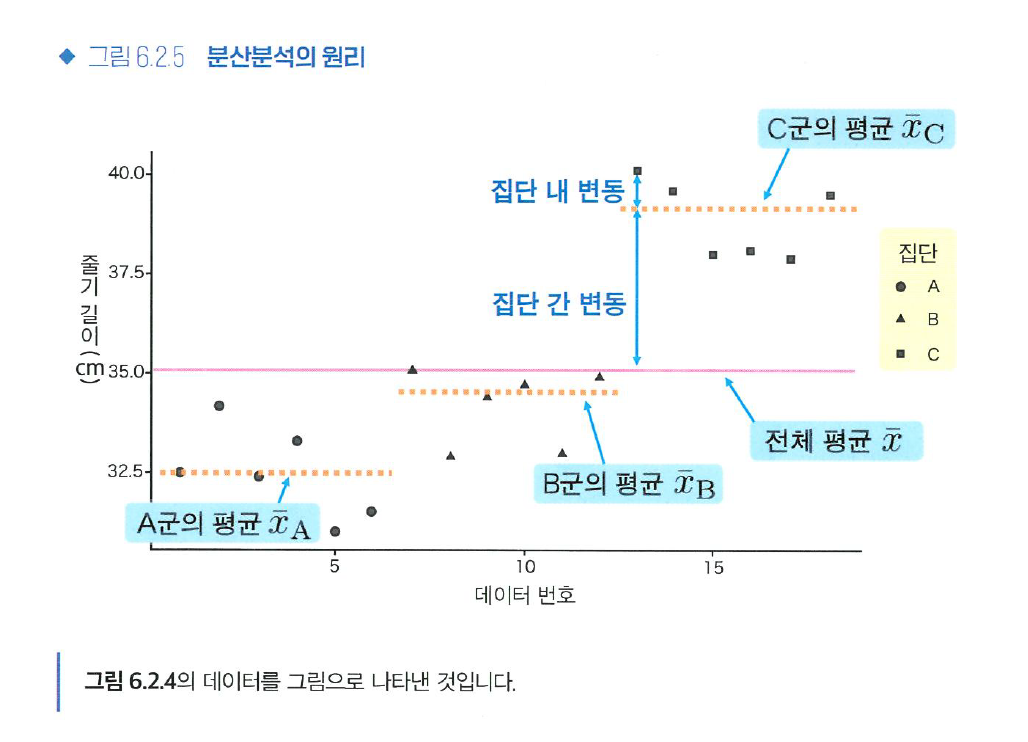
a. 분산분석의 원리 

 

- 전제

- 귀무가설: "모든 집단의 평균이 같다 (μA = μB = μC)"
- 대립가설: "적어도 한 쌍에는 차이가 있다"

 

 1. 집단의 차이를 무시하고 모든 데이터를 이용하여 전체 평균 x̄ 계산

 2. A, B, C 각 집단의 평균 계산

 3. 각 데이터의 차이 구함 (xi - x̄)

 4. 각 데이터의 분산을 '집단 내 변동 ', '집단 간 변동'의 2가지 요소로 분해

• 집단 내 변동: 같은 그룹 내에서 관측값 간의 차이로 인해 발생하는 변동 → 각 관측값이 해당 그룹의 평균으로부터 얼마나 떨어져 있는지 나타냄
  • 집단 내 변동은 원래 존재하는 무작위오차의 크기 (동일 조건에서의 데이터 퍼짐)
• 집단 간 변동: 그룹 평균 간의 차이로 인해 발생하는 변동 → 각 그룹의 평균이 전체 평균으로부터 얼마나 떨어져 있는지 나타냄
  
  • 집단 간 차이가 크다: 큰 데이터 퍼짐
  • 집단 간 차이가 작거나 없다: 작은 데이터 퍼짐 

 5. 검정통계량 생성: F-검정을 사용하여 (집단 간 변동) & (집단 내 변동)의 비율 계산

• 귀무가설이 올바르다는 가정하에, F분포라는 분포를 따름

 F값 = (평균적인 집단 간 변동) / (평균적인 집단 내 변동)

 

 6. F-검정의 결과를 바탕으로 p-값 구하고, 유의수준과 비교하여 귀무가설 기각 유무 판정

P값 = F값 이상으로 극단적인 값이 나올 확률

 

 

b. 다중비교 검정

• 분산분석을 통해 귀무가설을 기각시키고 대립가설을 채택하더라도, "적어도 한 쌍에는 차이가 있다"에서 어느 쌍에 차이가 있는지까지는 알 수가 없다
• 만약 어느 쌍에 차이가 있는지 알고 싶다면 다중비교라는 방법을 사용해야 한다
• 집단의 수가 늘어날수록 제1종 오류가 더 잘 나타나는데, 이 때 나타나는 다중성 문제를 회피하고자 다중비교 검정을 사용한다

1. 여러 가지 다중비교 방법

- 본페로니 교정

- 튜키 검정

- 던넷 검정

- 윌리엄스 검정

 

6.3) 비율 비교

범주형 데이터

- 지금까지는 양적 변수에 대한 모집단의 평균값 추정/ 모집단을 대상으로 가설을 세워 가설검정 진행

- 범주형 변수에서도 모집단의 파라미터를 추정/ 확률 P에 관련된 가설을 세워 검정할 수 있음

 

이항검정 (binomial test)

: 두 가지 범주 (성공/실패, 참/거짓 등)를 갖는 데이터를 분석할 대 사용

하나의 범주가 확률 P, 또 하나의 범주가 확률 1-P로 나타나는지를 조사

• example) 동전을 30번 던지는 설정
  • 귀무가설: "앞면이 1/2, 뒷면이 1/2 확률로 나온다"
  • 대립가설: "앞면이 1/2, 뒷면이 1/2 확률로 나오지 않는다"
• p 값 계산: 앞면 21번, 뒷면 9번 이상으로 극단적인 값이 나올 확률 계산
• if p < 0.05: 통계적으로 유의미하게 한쪽으로 치우쳤다고 판단 가능

 

카이제곱검정: 적합도검정 (chi-squared test)

: 주어진 범주형 데이터가 예상되는 분포와 일치하는지 여부를 확인하는 데 사용

• 귀무가설: "모집단은 상정한 이산확률분포이다."
• 대립가설: "모집단은 상정한 이산확률분포가 아니다"

a. 검정 과정

1. 귀무가설의 확률분포에서 얻을 수 있는 기대도수 계산

   * 기대도수 = (전체 개수) * (각 확률)

2. 관측값과 기대값 간의 차이 계산

  → (실제 출현도수 - 기대도수)^2 / * (기대도수) 를 더한 값

  → 카이제곱분포라는 확률분포를 따름

3. p값 도출

4. 유의수준과 비교하여 귀무가설을 기각 유무 판단

카이제곱검정: 독립성검정 (test of independence)

: 두 범주형 변수 간의 관계가 독립적인지를 검정

• 귀무가설: "OO과 OO은 독립적이다"
• 대립가설: "OO과 OO은 독립적이지 않다"

a. 검정 과정

 

1. 교차표를 사용하여 각 변수의 범주별 빈도 관찰

  → 한쪽 변수의 범주가 바뀌었을 때 다른 쪽 변수의 범주 비율이 달라지지 않았으면 두 변수는 독립적

2. 기대도수 계산

  → 기대도수: 분할표의 각 행과 열의 합 계산, 열의 합 비율을 기준으로 다시 배분

3. 관찰한 것을 기반으로 카이제곱 통계량 계산

4. p값 계산

5. 귀무가설 기각/채택 유무 판단